RC as an INTEGRATOR

Integrator 

Consider the output across the capacitor at high frequency i.e.

.

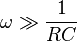This means that the capacitor has insufficient time to charge up and so its voltage is very small. Thus the input voltage approximately equals the voltage across the resistor. To see this, consider the expression for  given above:

but note that the frequency condition described means that

so

 which is just Ohm's Law.

Now,

so

,

 

Here RC=1u*1k=1ms. It means capacitor needs approximately 5RC=5m  to charge completely.However input pulse width is 2ms. so the waveform will be integrated version of input . SO RC acts as integrator.

IF c=0.5u RC=0.5m.So RC=2.5m.So capacitor will be charged almost completely as shown below

SIMULATION SOFTWARE :PSPICE . 

.